16th June 2020 , 2 min read
Gunnar Uldall's Tax Tariff
Gunnar Uldall wrote a a book with title "Die Steuerwende " in 1996.
1. Proposal. In this book he proposed the following tariff, $x$ is in DEM .
$$
t_u(x) = \begin{cases}
0 & \mbox{if } x\le12000 \\
0.08\left(x-12000\right) & \mbox{if } 12001\le x\le20000 \\
0.18\left(x-20000\right)+640 & \mbox{if } 20001\le x\le30000 \\
0.28\left(x-30000\right)+2440 & \mbox{if } x\ge30001
\end{cases}
$$
Of course, Gunnar Uldall opposed to add any solidary extra tax. Unfortunately, his proposal did not make it into law, although his proposal was well received in the public.
Gunnar Uldall makes a short historic reference to von Miquel 's tariff. The tariff from 1891 with $x$ is in Goldmark is given below.
$$
t_m(x) = \begin{cases}
0 & \mbox{if } x\leq900 \\
6 & \mbox{if } 900\lt x\leq1050 \\
9 & \mbox{if } 1050\lt x\leq1200 \\
12 & \mbox{if } 1200\lt x\leq1350 \\
16 & \mbox{if } 1350\lt x\leq1500 \\
21 & \mbox{if } 1500\lt x\leq1650 \\
26 & \mbox{if } 1650\lt x\leq1800 \\
31 & \mbox{if } 1800\lt x\leq2100 \\
36 & \mbox{if } 2100\lt x\leq2400 \\
44 & \mbox{if } 2400\lt x\leq2700 \\
52 & \mbox{if } 2700\lt x\leq3000 \\
60 & \mbox{if } 3000\lt x\leq3300 \\
70 & \mbox{if } 3300\lt x\leq3600 \\
80 & \mbox{if } 3600\lt x\leq3900 \\
92 & \mbox{if } 3900\lt x\leq4200 \\
104 & \mbox{if } 4200\lt x\leq4500 \\
118 & \mbox{if } 4500\lt x\leq5000 \\
132 & \mbox{if } 5000\lt x\leq5500 \\
146 & \mbox{if } 5500\lt x\leq6000 \\
160 & \mbox{if } 6000\lt x\leq6500 \\
176 & \mbox{if } 6500\lt x\leq7000 \\
192 & \mbox{if } 7000\lt x\leq7500 \\
212 & \mbox{if } 7500\lt x\leq8000 \\
232 & \mbox{if } 8000\lt x\leq8500 \\
252 & \mbox{if } 8500\lt x\leq9000 \\
276 & \mbox{if } 9000\lt x\leq9500 \\
30\lfloor (x-10500)/1000\rfloor + 330 & \mbox{if } 9500\lt x\leq30500 \\
80\lfloor (x-32000)/1500\rfloor + 1040 & \mbox{if } 30500\lt x\leq32000 \\
80\lfloor (x-32000)/2000\rfloor + 1040 & \mbox{if } 32000\lt x\leq78000 \\
100\lfloor (x-78000)/2000\rfloor + 2900 & \mbox{if } 78000\lt x\leq100000 \\
0.04\lfloor x/5000\rfloor\cdot5000 & \mbox{if } x\gt 100000 \\
\end{cases}
$$
By design this tariff has discontinuities. The first fixed values cannot easily be fitted with a linear, quadratic or cubic polynomial.
As can be seen by this tariff, it starts with a rate of less than one promille. Then slowly increases to at most four percent.
2. Current situation. The current tax tariff for $x$ in EUR as of 2020 is
$$
t_c(x) = \begin{cases}
0 & \mbox{if } x\le 9408 \\
\left(972.87{\lfloor x\rfloor-9408\over10000} + 1400\right){\lfloor x\rfloor-9408\over10000} & \mbox{if } 9409\le x\le 14532 \\
\left(212.02{\lfloor x\rfloor-14532\over10000} + 2397\right){\lfloor x\rfloor-14532\over10000} + 972.79 & \mbox{if } 14533\le x\le 57051 \\
0.42\lfloor x\rfloor - 8963.74 & \mbox{if } 57052\le x\le270500 \\
0.45\lfloor x\rfloor - 17078.74 & \mbox{if } x\ge270501
\end{cases}
$$
Final tariff is then
$$
\mbox{Taxes} = \lfloor t_c(x)\rfloor
$$
Add to this 5.5% solidarity extra tariff.
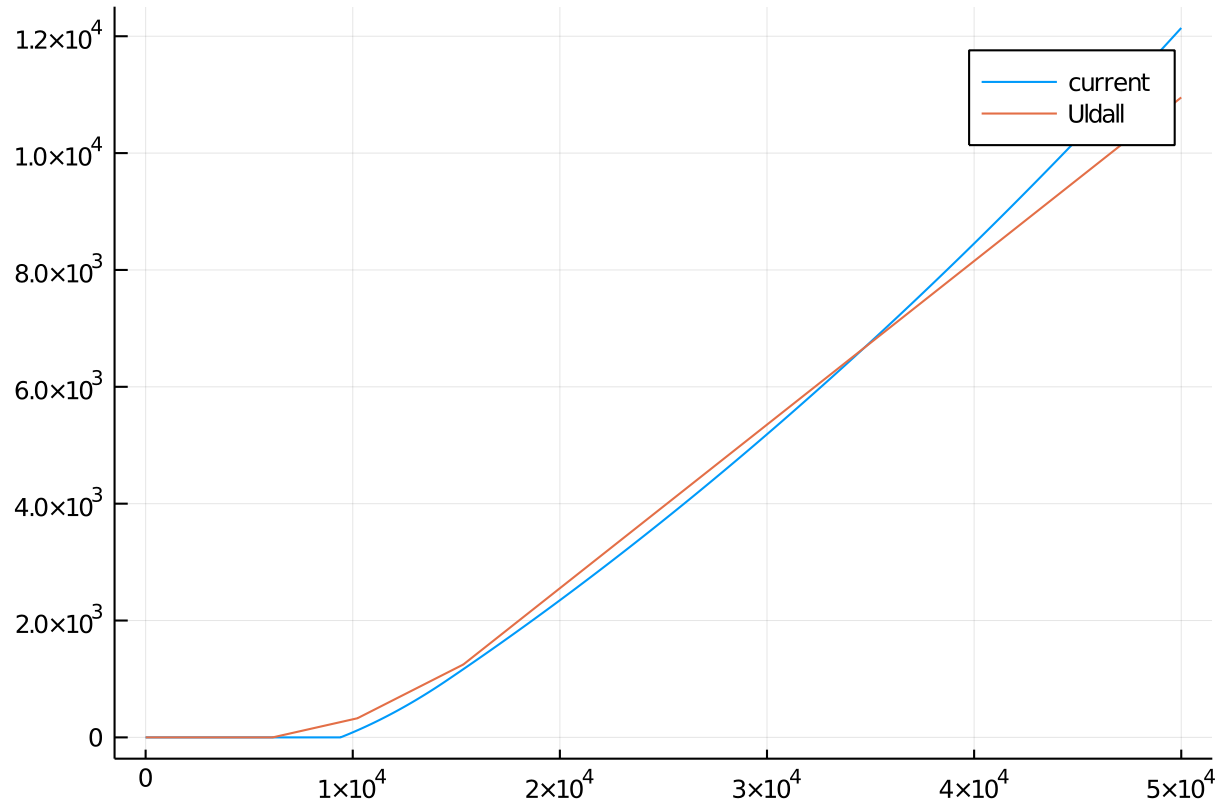
Graphical comparison of the two tariffs. First for amounts up to 50 kEUR.
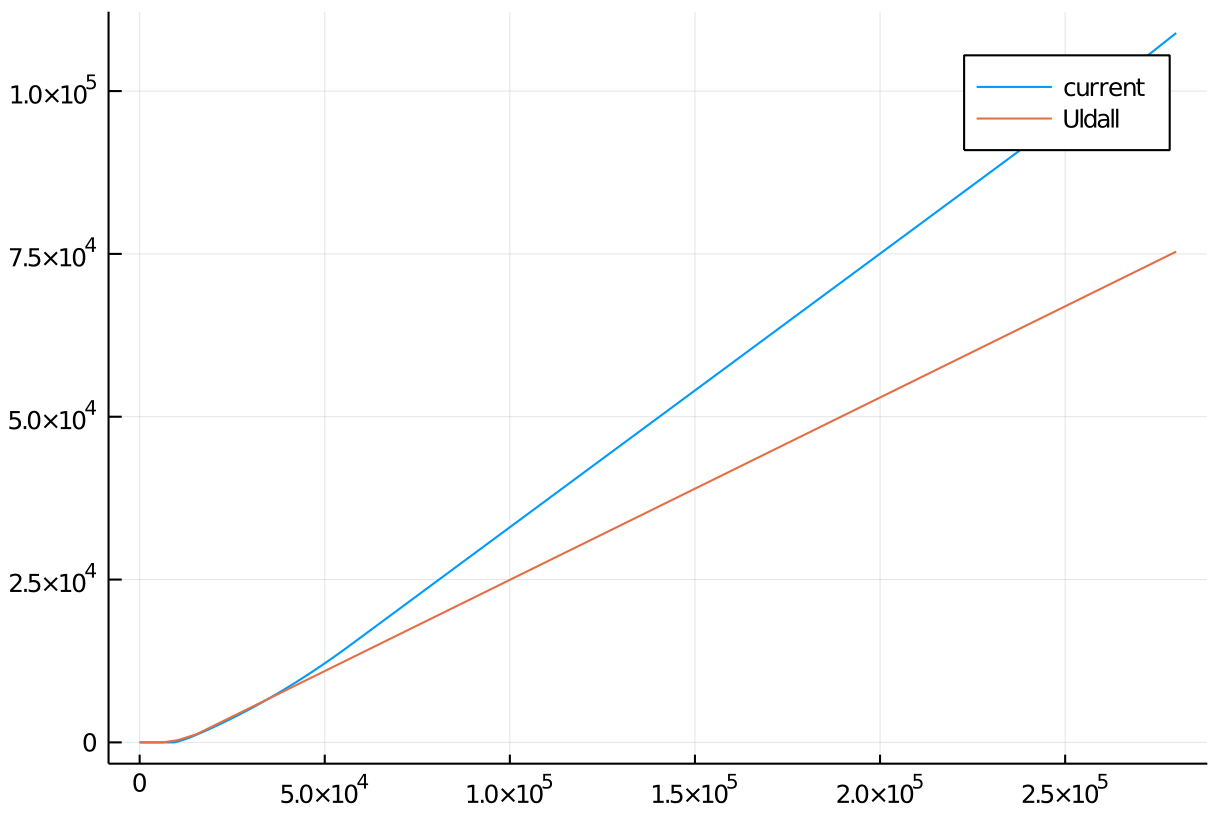
Now up to 280 kEUR.
Julia code is tariff.jl .