, 1 min read
Torricelli's Trumpet: Infinite Surface Area but Finite Volume
Just read on Torricelli's trumpet in Wikipedia. This states that there is a body having infinite surface but finite volume! That sounds contradictory at first.
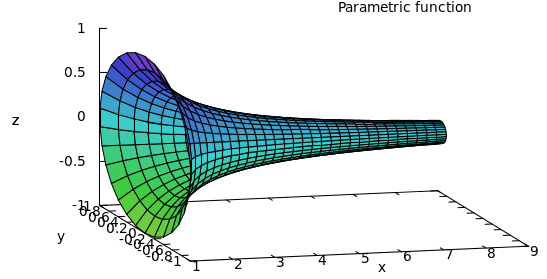
Function in question is
$$
y = 1 / x
$$
from $x=1$ to $a$.
Volume is
$$ V = \pi \int_1^a \left({1\over x^2}\right)\,dx = \pi\left(1-{1\over a}\right) $$
Surface is
$$ A = 2\pi \int_1^a {1\over x}\sqrt{1 + {1\over x^4}}\,dx \ge 2\pi \int_1^a {1\over x}\,dx = 2\pi\ln a $$
Above plot is from Maxima using:
plot3d( [x,1/x*sin(v),1/x*cos(v)], [x,1,8], [v,0,2*%pi] );