9th February 2021

Poisson Log-Normal Distributed Random Numbers

Task at hand: Generate random numbers which follow a lognormal distribution, but this drawing is governed by a Poisson distribution. I.e., the Poisson distribution governs how many lognormal random values are drawn. Input to the program are $\lambda$ of the Poisson distribution, modal value and either 95% or 99% percentile of the lognormal distribution.

From Wikipedia's entry on Log-normal distribution we find the formula for the quantile $q$ for the $p$-percentage of the percentile $(0<p<1)$, given mean $\mu$ and standard deviation $\sigma$:

$$ q = \exp\left( \mu + \sqrt{2}\,\sigma\, \hbox{erf}^{-1}(2p-1)\right) $$

and the modal value $m$ as

$$ m = \exp\left( \mu - \sigma^2 \right). $$

So if $q$ and $m$ are given, we can compute $\mu$ and $\sigma$:

$$ \mu = \log m + \sigma^2, $$

and $\sigma$ is the solution of the quadratic equation:

$$ \log q = \log m + \sigma^2 + \sqrt{2}\,\sigma\, \hbox{erf}^{-1}(2p-1), $$

hence

$$ \sigma_{1/2} = -{\sqrt{2}\over2}\, \hbox{erf}^{-1}(2p-1) \pm\sqrt{ {1\over2}\left(\hbox{erf}^{-1}(2p-1)\right)^2 - \log(m/q) }, $$

or more simple

$$ \sigma_{1/2} = -R/2 \pm \sqrt{R^2/4 - \log(m/q) }, $$

with

$$ R = \sqrt{2}\,\hbox{erf}^{-1}(2p-1). $$

For quantiles 95% and 99% one gets $R$ as 1.64485362695147 and 2.32634787404084 respectively. For computing the inverse error function I used erfinv.c from lakshayg.

Actual generation of random numbers according Poisson- and lognormal-distribution is done using GSL. My program is here: gslSoris.c.

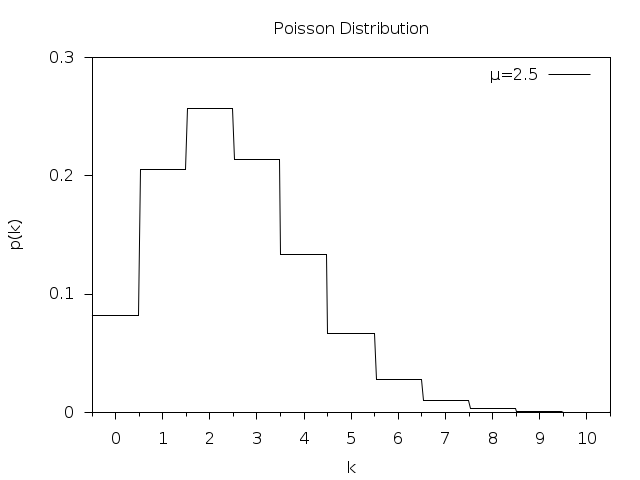
Poisson distribution looks like this (from GSL documentation):

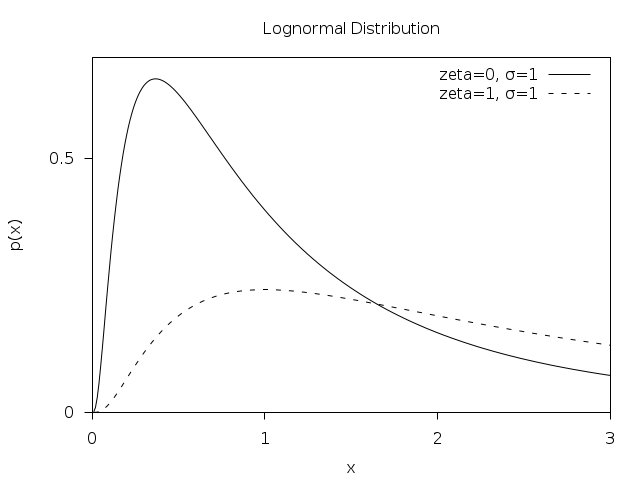
Lognormal distribution looks like this (from GSL):

Categories: mathematics
Tags: ,
Author: Elmar Klausmeier