, 38 min read
Tendler-like Formulas for Stiff ODEs
Abstract. This paper proves a convergence result for a general class of methods for the solution of ordinary differential equations (initial value problems). The proof uses standard results from the theory of matrix polynomials. We present new cyclic linear multistep formulas of orders 3 to 9 for stiff equations, which, order by order, outperform the cyclic composite multistep methods of Tendler with respect to the Widlund-wedge angle and Widlund-distance. The Tendler formulas had already outperformed the BDF order by order. We present numerical accuracy comparisons on Dahlquist’s and Runge’s test equations with the BDF, the original Tendler, the new methods, and the Tischer methods.
Subject Classification: Mathematics Subject Classification 65L04 65L06; CR: G.1.7.
- 1. Introduction
- 2. Consistency and stability
- 3. Convergence result
- 4. New cyclic linear multistep formulas
- 5. Numerical results
- 6. Summary and conclusions
- 7. References
1. Introduction
We consider the numerical solution of the ordinary differential equation, the initial value problem
Assume that $f:[t_0,t_\text{end}]\times\mathbb{C}^n \to \mathbb{C}^n$ is Lipschitz-continuous in $y$ for all $t$, and continuous in $t$. We will use cyclic linear multistep methods for this, i.e., we will employ a fixed set of linear multistep methods and cycle through them.
Cyclic linear multistep methods are attractive for a number of reasons:
- They are not subject to Dahlquist's first and second barriers.
- They share the same low overhead per step as linear multistep methods.
- They offer more parameters to attain desirable stability or accuracy properties than linear multistep methods.
Below is an example of an order-four cyclic composite method, which we call eTendler4 (enhanced Tendler4). It cycles through three different linear multistep methods for some fixed step size $h\in\mathbb{R}$, $m=1,2,\ldots$:
The first stage of eTendler4 is the standard BDF4 (the classic backward differentiation formula of order 4). Each stage is a 4-step linear multistep formula.
In addition to the initial value $y_0$, the above difference method needs three starting values $y_1$, $y_2$, and $y_3$ and will then produce discrete values $y_k$ for $k=4,5,\ldots$, as approximations of order ${\mathcal O}(h^4)$ to the desired function $y$, $\dot y_k = f(t_k,y_k)$, $t_k=t_0+kh$. These starting values can be generated using lower-order methods with fewer required starting values and a smaller step size $|h|$.
In a later chapter it will be shown that the above method converges for sufficiently small $|h|$ for a wide range of functions $f$.
The difference equation above can be expressed in matrix-vector form:
with
and
and
Stability of this cyclic method is now governed by the two matrix polynomials
All stages in eTendler4 are implicit and must therefore be solved iteratively (fixed-point or Newton).
The stages of a composite method might be explicit or implicit. They might have different orders, and might require a different number of starting values.
2. Consistency and stability
1. Consider the multistep method
and
The consistency conditions are:
The consistency matrix $C_{p,k}$ for a linear $k$-step method of consistency order $p$ is given by the following equation
2. Theorem: The following eight propositions are equivalent. Therefore any of these statements can be used as a definition for consistency of order $p$.
(1) $C_{p,k} \binom{\alpha}{\beta}= {\bf0}$, so $(\alpha,\beta)^\top\in\ker C_{p,k}$.
(2) $\sum_{i=0}^k \alpha_i i^q = q\sum_{i=0}^k \beta_i i^{q-1}$, for $q=0,1,\ldots,p$.
(3) $\rho(e^h)-h\sigma(e^h)={\mathcal O}(h^{p+1})$, for $h\to 0$.
(4) $\zeta=1$ is a zero of multiplicity at least $p$ of the function
so $\rho(\zeta)/\ln\zeta=\sigma(\zeta)+{\mathcal O}\bigl((\zeta-1)^p\bigr)$, for $\zeta\to 1$.
(5) $L(f,t,h)={\mathcal O}(h^{p+1}),\quad\forall f\in C^{p+2}(G,\mathbb{C}{})$.
(6) The monomials up to the degree $p$ lie in the kernel of the $h=1$ cut of $L$; therefore $L(t^i,t_0,1)=0$, for $i=0,1,\ldots,p$.
(7) $L(f,t_0,h)={\mathcal O}(h^{p+1})$, for the special function $t\mapsto f(t)=e^t$.
(8) $L(y,t_0,h)=c_{p+1}h^{p+1}y^{(p+1)}(t_0)+{\mathcal O}(h^{p+2})$ with
The factor $c_{p+1}$ is called the unscaled error constant.
Proof: Mostly trivial reformulations. See Hairer/Wanner/Norsett (2008), Thm. III.2.4. ☐
3. Our composite method is
$\varphi(\cdot)$ also depends on $h$, $t_{n+i}$, and $f$, but for brevity we omit that. This general method is called general linear method in Butcher (2016) and Hairer/Wanner/Norsett (2008). The characteristic polynomial is
The stability region of a method is the area
This set is not necessarily connected, i.e., it might contain holes. See, for example, the two block-implicit methods of order 8 and 10 from Bickart/Picel (1973).
The stability mountain is the set
This mountain is interesting for observing how fast $|\mu|$ decays, i.e., the gradient.
4. Definition. Slightly deviating and expanding from Tendler/Bickart/Picel (1978). For real values $\alpha\ge0$, $\delta\ge0$, $r\ge0$, let
- A method is $D$-stable if the Jordan triple for the matrix polynomial $Q(\mu,0)$ has all its eigenvalues in the closed unit disc with all eigenvalues of magnitude 1 lying in $1\times1$ blocks, see Butcher (2016), Thm 142C.
- The eigenvalues not equal to 1 for $Q(\mu,0)$ with the greatest magnitude are called the parasitic roots.
- A method is $A[\alpha]$-stable if ${\mathcal A}[\alpha]$ is a subset of the stability region.
- The largest $\alpha$ for which a method is $A[\alpha]$-stable is called the Widlund-wedge angle $\alpha$.
- A method is $S[\delta]$-stable if ${\mathcal S}[\delta]$ is a subset of the stability region.
- The smallest $\delta$ for which a method is $S[\delta]$-stable is called the Widlund-distance $\delta$.
- If $\alpha=90^\circ$ or $\delta=0$ then the method is called $A$-stable.
- An $A[\alpha]$-stable method with the additional property that for $\mathop{\rm Re}\nolimits H\to-\infty$ all $|\mu|<r$ is called $A_\infty^r[\alpha]$-stable. The smallest $r$ is of interest.
- An $S[\delta]$-stable method with the additional property that for $\mathop{\rm Re}\nolimits H\to-\infty$ all $|\mu|<r$ is called $S_\infty^r[\delta]$-stable.
- For $r<1$ we abbreviate with $A_\infty[\alpha]$- and $S_\infty[\delta]$-stable. For $r=0$ the limit $r\to 0$ is meant. An $A_\infty^0[90^\circ]$-stable method is called $L$-stable, see Hairer/Wanner (2010), definition 3.7.
5. Examples. The above stability characteristics manifest in all shapes and forms.
- The explicit Euler method, $y_{n+1} = y_n + h f(t_n,y_n)$, is $D$-stable but not $A$-stable, nor $A[\alpha]$-stable.
- The implicit Euler method (=BDF1), $y_{n+1} = y_n + h f(t_{n+1},y_{n+1})$, and the BDF2 are $D$-stable and $A$-stable.
- The BDF$i$ are $D$-stable for $i=1,\ldots,6$, and are unstable for all $i\ge7$, see Hairer/Wanner/Nørsett (2008), III.3, Thm 3.4.
- The BDF$i$ ($i=1,\ldots,6$) are $A_\infty^0[\alpha]$-stable with $\alpha$ being 90°, 90°, 86.03°, 73.35°, 51.84°, 17.84°, respectively, see Akrivis/Katsoprinakis (2020).
- All Tischer cyclic composite formulas, see Tischer (1983) and Tischer/Sacks-Davis (1983), are $A_\infty^0[\alpha]$-stable and $S_\infty^0[\delta]$-stable and have equal to zero parasitic roots. These properties are highly desirable for the integration of stiff systems.
- The 5-step cyclic linear multistep method with 5 stages of order seven from Mihelcic/Wingerath (1981) is $A[44.8^\circ]$- and $S[6]$-stable. The $\alpha$ given in Mihelcic/Wingerath (1981) is slightly smaller.
- The linear multistep formula of order nine from Gupta (1985) used in DSTIFF is $S_\infty^{0.989}[2.086]$-stable.
- The DSTIFF formula of order 10 from Gupta (1985) is $A_\infty^{0.878}[63.74^\circ]$-stable.
- The new formulas eTendler8 and eTendler9 are $S_\infty^0[\delta]$-stable but not $A[\alpha]$-stable.
3. Convergence result
The proof of the convergence result is conducted in the setting of matrix polynomials, see Gohberg/Lancaster/Rodman (1978) or Gohberg/Lancaster/Rodman (2009).
For the differential equation we can confine ourselves to the scalar case $n=1$, i.e., $\mathbb{C}$ instead of $\mathbb{C}^n$. Otherwise we would have to add $A_i\otimes I_{n\times n}$, and $B_i\otimes I_{n\times n}$, etc. everywhere.
6. Notation. Let $(P_1,C_1,R_1)$ be the first companion triple for the matrix polynomial
of degree $\ell\ge1$.
Let $\mathopen|t_\text{end} - t_0\mathclose|\ne0$. The step size $h$ is such that $\mathopen|t_\text{end}-t_0\mathclose| / \mathopen|h\mathclose|$ is an integer. $N$ is defined by $N\mathopen|h\mathclose| = \mathopen|t_\text{end} - t_0\mathclose|$.
Let
Let $I=I_{k\times k}$. The first companion matrix is
Further
and
Let
7. Definition. Let $T$ be an arbitrary square matrix of size $k\times k$. The bidiagonal operator $[T]$ for the matrix $T$ of size $(N+1)k\times(N+1)k$, is defined as follows:
See Skeel (1976).
For the product we have: $[C_1]^{-1} \boro \in \mathbb{C}^{(N+1)k\ell \times (N+\ell)k}$.
Let $(X,T,Y)$ be an arbitrary standard triple. Due to biorthogonality we have
with the block-Hankel-matrix $B$
See Gohberg/Lancaster/Rodman (2009), Prop. 2.1.
Further
and
The special handling of the block matrix for $\boro$ and $\ovbf Y$ in the first “diagonal element” has its root in the solution representation of the difference equation for matrix polynomials of the form
For the case $\ell=1$ we have $\rho(\mu)=I\mu-A$ and the two matrices $P_1$ and $R_1$ reduce to the identity matrices of size $n\times n$. The biorthogonality relation reduces to $X=Y^{-1}$ or $X^{-1}=Y$.
8. Theorem: (Discrete Lemma of Gronwall) Let $0\le\eta_0\le\eta_1\le\ldots\le\eta_m$ be $(m+1)$ positive numbers. Furthermore $\delta\ge0$, $h_j\ge0$ and $x_{j+1}=x_j+h_j$. Assume
Then
Proof: See Werner/Arndt (1986). The case $\delta=0$ is simple, due to $e^0=1$. Hence, let $\delta>0$. Starting the induction with $j=0$ is obvious, again due to $e^0=1$. We perform induction from $j$ to $j+1$, assuming $\delta>0$. We have
This is so because for the sum in parentheses we can estimate (the sum of a strictly monotonically increasing function)
☐
9. Theorem: (Properties of $\dcol$, $\drow$, $\diag$, $[\cdot]$) We have
- $\dcol A_\nu B_\nu = \diag A_\nu{\mskip 5mu}\dcol B_\nu$.
- $\dcol A_\nu B = \left(\dcol A_\nu\right) B$; right distributivity of $\dcol$-operator.
- $\drow A_\nu B_\nu = \drow A_\nu{\mskip 5mu}\diag B_\nu$.
- $\drow AB_\nu = A{\mskip 3mu} \drow B_\nu$; left distributivity of $\drow$-operator.
- $\diag A_\nu B_\nu = \diag A_\nu{\mskip 5mu}\diag B_\nu$.
- $\left[S^{-1}TS\right] = \diag S^{-1}{\mskip 3mu} \left[T\right]{\mskip 3mu} \diag S$.
- $\left[S^{-1}TS\right]^{-1} = \diag S^{-1}{\mskip 5mu}\left[T\right]^{-1} \diag S$.
Proof: Trivial computations. ☐
10. Theorem: (Solution of difference equation) The general solution of the difference equation
is
Proof: See Gohberg/Lancaster/Rodman (2009), Thm. 1.6. ☐
11. Theorem: (Representation theorem) Prerequisites: $\hat u_n$ and $u_n$ are the solutions of the two difference equations
The “disturbances” $r_{n+\ell}$ correspond to $\hat u_{n+\ell}$. We will use
The difference equation for $\hat u_n$ has the starting values $\hat u_i := u_i + r_i$, for $i=0,\ldots,\ell-1$. Let $\delta_i := r_i$, for $i=0,\ldots,\ell-1$, and $r_\nu := \delta_\nu := \hat\delta_\nu := 0$, for $\nu>N$.
Proposition:
Proof: Follows immediately from the previous theorem. ☐
12. Theorem: Prerequisite: Let $C_1^i := {\bf0} \in \mathbb{C}^{k\ell\times k\ell}$, when $i<0$.
Proposition: The reduced stability functional is norm-equivalent to the original stability functional, i.e.,
Proof: In two parts. We estimate each against the other.
(1) The estimation $\left|\bopo [C_1]^{-1} \boro \bfR\right| \le \left|\bopo\right| \left|[C_1]^{-1} \boro \bfR\right|$ is obvious. The row-norm of $\bopo$ is independent of $N$.
(2) We use
due to
We can "extract" $C_1^{\ell-1}$ because the $\sup$-norm for $\left| \bopo [C_1]^{-1} \boro \bfR \right|$ still goes over all rows. Finally
due to $r_\nu := 0$, for $\nu>N$. ☐
13. Theorem: (Estimation theorem) Prerequisite: Let $\varphi(\cdot)$ be Lipschitz-continuous in each component with Lipschitz constant $K_i$. The values $\delta_{\nu+\ell}$ and $\hat\delta_{\nu+\ell}$ are as above.
Proposition:
Proof: For $\nu=0,\ldots,n-1$ we have
For ease of notation $\delta_\nu \gets \mathopen|\delta_\nu\mathclose|$ and $\hat\delta_\nu \gets \mathopen|\hat\delta_\nu\mathclose|$. Hence,
Summation and estimate shows the first claim. The second estimate follows from the first. ☐
14. Main theorem: Prerequisites: The function $\varphi$ is Lipschitz-continuous in each component with Lipschitz constants $K_i$, i.e.,
The powers of the matrix $C_1$ are bounded by $D$, $\left|C_1^\nu\right|\le D$, $\forall\nu\in\mathbb{N}$. Let $\xi$ and $\hat\xi$ be
The value $\hat\xi$ is a multivariate function: $\hat\xi=\hat\xi(P_1,D,R_1,K_0,\ldots,K_\ell)$.
Assume
Proposition: (1) The two difference equations
have a unique solution $u_{n+\ell}$ for each $n$ , and $\hat u_{n+\ell}$.
(2) For the maximal norm deviation $\left|\hat u_n-u_n\right|$ we have the two-sided estimation with respect to the error terms $r_n$,
We use $U=(u_1,\ldots,u_N)$, and $\hat U=(\hat u_1,\ldots,\hat u_N)$.
(3) The positive constants $c_i$, for $i=1,2,3$, are given by
(4) The estimate by (2) is independent from the choice of standard triple, i.e.,
for two arbitrary standard triples $(X_1,T_1,Y_1)$ and $(X_2,T_2,Y_2)$ for the matrix polynomial $\rho$.
(5) The reduced functional $\left|[C_1]^{-1} \boro \bfR \right|$ is also a stability functional and equivalent to the unreduced functional, independent of $N$, i.e.,
(6) Reduced stability functionals are each equivalent when changing standard triples. They are not necessarily equal. We have
Proof: For abbreviation, we use
For (1): For each $n$ both difference equations can be written as
These are contractive if $\mathopen|h\mathclose| K_\ell < 1$. Therefore, we have uniqueness due to $\mathopen|h\mathclose|\xi<1$.
For (2): a) According to the representation theorem
Here we used
of the above estimation theorem. We employed $N\mathopen|h\mathclose| = \mathopen|t_\text{end}-t_0\mathclose|$ and finally $\sum_{\nu=0}^n \mathopen|\delta_\nu\mathclose| \le N\sup_{\nu=0}^{n-1} \mathopen|\delta_\nu\mathclose|$. Multiplying by
then this gives the first inequality from (2), and also gives $c_1$.
b) Again using the representation theorem and using norms
We make use of the estimation theorem once more
As $\mathopen|h\mathclose|<1/\xi$, we have $1-\mathopen|h\mathclose|\xi>0$. Using the discrete lemma of Gronwall and using
we get the estimate
This shows the constant $c_2$. The constant $c_3$ results from a typical estimation.
For (4): The standard triple $(X_1,T_1,Y_1)$ is similar to the standard triple $(X_2,T_2,Y_2)$ iff
or
Now we have
For (5): This was already proved.
For (6): As in (4)
Multiplying from the left with $\diag_{\nu=0}^N S^{-1}$ then this gives
Therefore, both stability functionals are equivalent. ☐
Similar results can be found in Albrecht (1978) and Albrecht (1985), who also analyzes the left eigenvectors, which under some circumstances allow a higher convergence rate.
With the main theorem we now have the promised convergence result for a consistent method, i.e., we have the classical result:
- Consistency + $D$-Stability $\Rightarrow$ Convergence.
4. New cyclic linear multistep formulas
We now stick to cyclic linear multistep methods of the form
Building on the work of Tendler (1973) we combine the base formulas given in his chapter 4.2 and use the same restrictions R1-R4. Linear combinations of elements in the kernel of $C_{p,k}$ are also in the kernel.
15. Restrictions. Now for $i=1,\ldots,\ell$:
- R1. $\alpha_{ij} = \beta_{ij} = 0,$ for $i<j$
- R2. $\beta_{ij} = 0$ for $j\le0$ and $\beta_{ii}\ne0$
- R3. $\alpha_{ij} = 0$ for $j < -k + i$
- R4. $p_i \ge k$, where $p_i$ is the consistency order of the $i$-th stage
By design of R1-R4 all Tendler-like cycles start with the BDF of the same order. Further, if the Tendler-like formula is $A[\alpha]$-stable, it is also automatically $A_\infty^0[\alpha]$-stable.
Restriction R3 has its origin in an implementation detail of STINT, where the predictor for $y_{m\ell+i}$ for each stage $i$ in the cycle is built only from the backward differences of $y_{m\ell+i-1}$, see Tendler/Bickart/Picel (1976). In principal, however, at each stage $i>1$, all the previous values are available. In contrast, the Tischer formulas are not subject to the restriction R3.
16. Characteristics. The new cyclic linear multistep formulas are called eTendler3–9 (enhanced Tendler3–9). These kind of formulas are a natural extension of the BDF to cyclic form. From an implementation viewpoint, they are advantageous because each cycle requires no derivatives from the previous cycle. Therefore, no interpolation and storage for $f(t_n,y_n)$-values is required. In contrast, Tischer's formulas need storage and interpolation for both, $y_n$ and $f(t_n,y_n)$.
It is worth noting that although the new formulas all start with BDF$i$ and the BDF$i$ are not $D$-stable for $i\ge7$, the new cyclic formulas are all $D$-stable. In a cyclic method one or all constituent multistep methods might be unstable, nevertheless the cycle itself can be $D$-stable.
For Tischer's formulas see Tischer (1983), Tischer/Sacks-Davis (1983), and Tischer/Gupta (1985). All Tischer formulas have a cycle length of two.
While Tendler apparently searched in an entirely manual way, we searched in an incremental and random machine-assisted way. I.e., we searched in a hypercube of the parameter space by either providing a starting point, or letting those starting points be chosen by a random number generator. Our search criteria were Widlund-wedge $\alpha$, Widlund-distance $\delta$, and parasitic root modulus.
The formulas from Tendler from 1973 were our baseline. Clearly, we wanted to improve them, or at least find possible limits. So in table 1 we summarize their characteristics:
- $p$ is the convergence order
- $\ell$ is the cycle length of the Tendler formulas
- abs(root) is the magnitude of the parasitic root
- $\alpha$ is the Widlund-wedge angle
- $\delta$ is the Widlund-distance
| $p$ | $\ell$ | abs(root) | $\alpha$(Tendler) | $\delta$(Tendler) | $\alpha$(Tischer) | $\delta$(Tischer) | |
|---|---|---|---|---|---|---|---|
| 1 | 3 | 0 | 90° | 0 | 90° | 0 | |
| 2 | 3 | 0.333333333 | 90° | 0 | 90° | 0 | |
| 3 | 3 | 0.55371901 | 89.427° | 0.004776 | 90° | 0 | |
| 4 | 3 | 0.35406989 | 80.882047° | 0.244157 | 90° | 0 | |
| 5 | 4 | 0.42931855 | 77.477315° | 1.421472 | 86.649352° | 0.040844 | |
| 6 | 4 | 0.52827598 | 63.245842° | 2.933167 | 76.311756° | 0.280752 | |
| 7 | 4 | 0.66669430 | 33.531759° | 10.179501 | 57.663061° | 0.959187 | |
| 8 | n/a | n/a | n/a | n/a | 22.149242° | 2.534082 |
The new cyclic linear multistep formulas have better stability characteristics order by order than the original Tendler formulas. They in turn have better stability characteristics than the BDF.
| $p$ | $\ell$ | abs(root) | $\alpha$(new) | $\delta$(new) | Comment |
|---|---|---|---|---|---|
| 3 | 3 | 0.70756795 | 89.72423° | 0.00164 | worse root modulus, better $\delta$ |
| 4 | 3 | 0.28351644 | 84.91216° | 0.07106 | better modulus, better $\alpha$, better $\delta$ |
| 5 | 3 | 0.48870093 | 77.81321° | 0.42370 | shorter cycle length, better $\alpha$, better $\delta$ |
| 6 | 4 | 0.29026688 | 71.63806° | 1.03854 | better modulus, better $\alpha$, better $\delta$ |
| 7 | 4 | 0.57300425 | 55.13529° | 3.87902 | better modulus, better $\alpha$, better $\delta$ |
| 8 | 4 | 0.61600197 | none | 15.05503 | no other formula with $\alpha>0.1$ found |
| 9 | 5 | 0.76270334 | none | 38.22753 | cycle length > 4 seems to be required |
17. Higher order. While a formula not being $A[\alpha]$-stable is of limited value for a pure stiff ODE solver, it is nevertheless of interest for a type-insensitive code, see Shampine (1982) and Norsett/Thomsen (1986), switching between fixed point and Newton iteration. The type-insensitive code LSODA from Petzold (1983) has been found useful and competitive in Städter et al (2021). Higher order methods are required for orbit calculations with higher precision, see Montenbruck/Gill (2000) chapter 4.1.6.
The stability mountain of the new order 3 method eTendler3 is shown in the first figure.
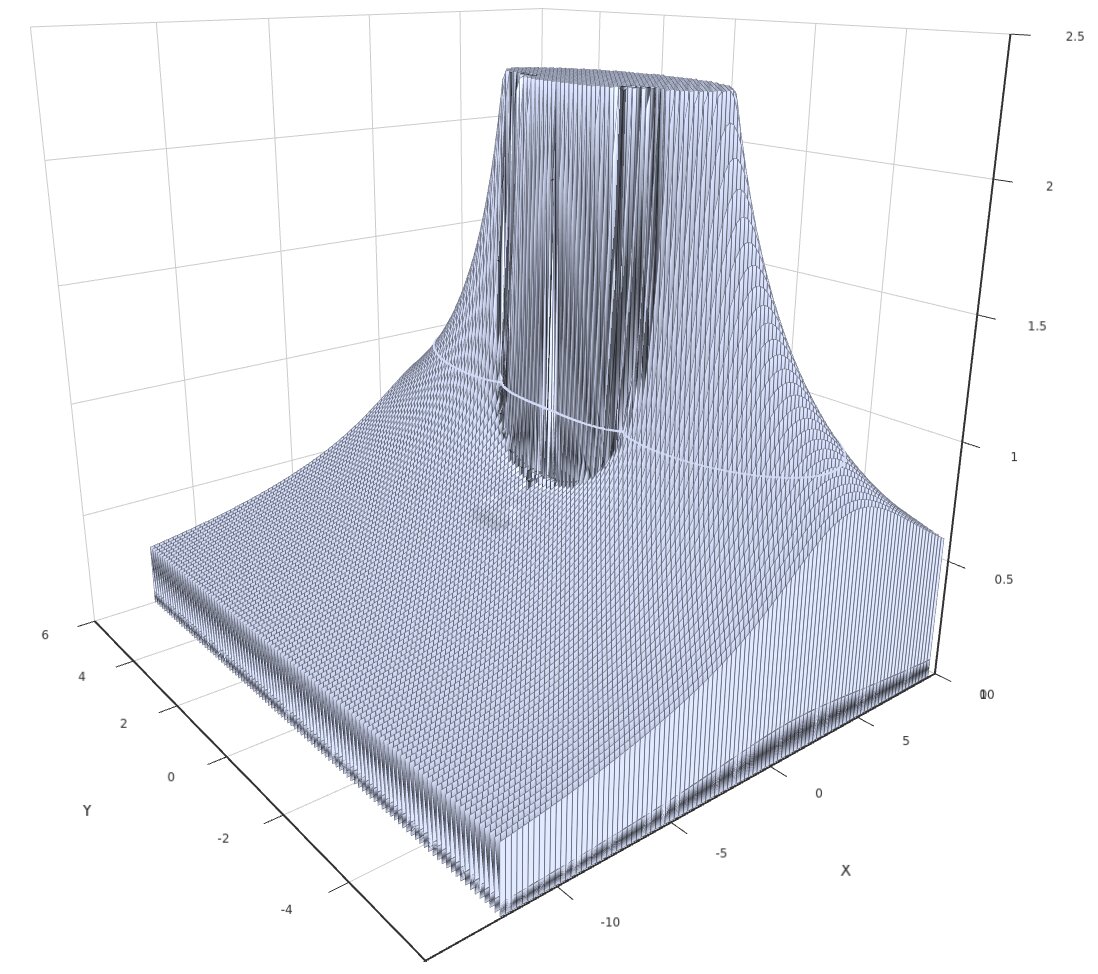
Our search results based on restrictions R1-R4 are as follows:
- We didn't find any formula of order 8 and higher with an $\alpha$ of any significance, even when allowing for a huge number of stages. It is therefore conjectured that there aren't any methods of this kind.
- We didn't find any formula of order 3 and 4 which actually is $A$-stable, in contrast to Tischer's results. We conjecture that there isn't any.
18. The formulas. $c_{i,p+1}$ is the unscaled error constant of the $i$-th stage. $\eta_{i,p+1}$ is the scaled error constant for the eTendler formulas. Likewise, $\eta^o_{i,p+1}$ are the scaled error constants for the original Tendler formulas, and $\eta^T_{i,p+1}$ are the scaled error constants for the Tischer formulas.
The minus-sign is only there as most formulas in this manuscript have negative values.
For linear multistep methods and cyclic methods the $\alpha_{ii}$ cannot be zero. However, for a block-implicit method the $\alpha_{ii}$ can be zero, see the order 2, 4, 6, 8 and 10 methods in Bickart/Picel (1973). More on the scaled error constant in Tischer (1983), appendix B, and Albrecht (1985), chapter 6.
The error constants are rounded to five digits after the decimal point. The coefficients of the formulas are exact.
Order 3 and 4.
Order 5 and 6. $\eta^o_{4,p+1} = 0.10320$ for $p=5$ where Tendler's formula needs four stages.
Order 7.
Order 8.
Order 9.
5. Numerical results
We will now use various formulas and conduct more than 5000 numerical tests. Before implementing new formulas in a variable step size and variable order computer code with convergence tests, nonlinear equation solver, interpolation, dozens of heuristics, type-insensitive switching logic, etc., we want to ascertain that the formulas work as intended. Creating such a computer code is a substantial software development effort.
The first parameterized differential equation tests the resilience against stiffness. The second differential equations tests for accuracy in the presence of large modulus of the higher derivatives.
19. Dahlquist's equation. We tested the BDF, Tendler's formulas, new Tendler-like formulas, and Tischer's formulas on the classical test equation
We used
The radius is fixed to $r=100$, and $\varphi$ varies from 5° to 90° in steps of 5°. $\varphi$ directly tests the Widlund-wedge angle of the formula.
The step size $h$ for each formula is chosen as $h=-0.1$, then $h=-0.01$, finally $h=-0.001$.
The above differential equation is now solved with the following formulas:
- BDF of order 1–6
- Original Tendler formulas of order 3–7. Note: Tendler's formulas of order 1 and 2 are just the BDF1 and BDF2.
- New Tendler-like formulas of order 3–9
- Tischer's formulas of order 2–8 using $s=0$, see Tischer/Sacks-Davis (1983) for the meaning of $s$
This creates 1350 data points. Multiplying by two hardware architectures and two precisions yields 5400 records.
20. Global error. We report the summed global error computed as
Computations were done in double precision (double complex in the C programming language).
Results are here.
As the global error $|y(t_i) - y_i|$ per step varies wildly between $10^{-324}$ and $10^{+304}$, we computed
Less is better. That is what is shown in the second figure.

One can clearly see that the higher-order methods quickly lose precision when a higher Widlund-wedge angle is required. This is the reason why none of the computer codes GEAR, EPISODE, LSODE and CVODE use BDF6. However, in reality, this is mainly a problem for the step size and order control segment to properly switch order.
The second figure also demonstrates that the Tischer formulas produce larger global errors. This is to be attributed to the error constants being an order of magnitude larger than the error constants of the Tendler formulas. That explains why the program ODIOUS, which uses the Tischer formulas, needs a smaller step size, and therefore needs more steps. This is reflected in the results in Tischer/Gupta (1985).
Since Gaffney (1984) noted a sensitivity regarding the chosen precision, especially in STINT, which implements Tendler's formulas,
we repeated the above tests in single precision (float complex in the C language) and on two CPU architectures (AMD Ryzen 5700 and ARM Cortex A77).
The qualitative results did not differ in any way.
We henceforth conclude that the discontinuity and sensitivity of the step size and order control segment are the reason for the observed behavior
in line with the remarks in Gaffney (1984).
21. Runge's equation. The test equation is
It has the exact solution $y(t) = 1/(1+t^2)$.
This is a numerical quadrature problem and not really a differential equation. This is Runge's function showcasing Runge's phenomenon.
For the numerical solution we used the step sizes $h=0.1$, $h=0.01$, and $h=0.001$.
Running the same formulas from above creates 75 data points. Multiplying by two precisions gives 150 records.
All formulas produce accurate results and the error is always considerably smaller than one. We therefore show
Higher is better.
The third image shows the results for quadruple precision (long double).

From an accuracy point of view the formulas eTendler6-9 are outperformed by BDF6 and Tendler7 for the step size $h=0.001$. For $h=0.01$ eTendler8 shows the best accuracy.
The Tischer formulas again fall short of expectations and produce larger errors than all the other methods. This is to be explained by their larger error constants multiplied by the large magnitude of the higher derivatives of the Runge function. This is in line with the results reported in Tischer/Gupta (1985) where the ODIOUS program on average needs 50%-100% more steps and function evaluations than LSODE (based on BDF) excluding problem B5.
6. Summary and conclusions
We have given a convergence proof for general linear methods in the setting of matrix polynomials. Matrix polynomials are a versatile medium to analyze cyclic linear multistep methods.
We have extended the work of Tendler and found new cyclic linear multistep formulas with enhanced Widlund-wedge angle and Widlund-distance. It is conjectured that by lifting restriction R3 we might find even more enhanced formulas.
By comparing the error constants we explain why the Tischer formulas produce larger global errors.
Conflict of interest: There is no conflict of interest.
7. References
- Akrivis, G., Katsoprinakis, E.: Maximum angles of $A(\vartheta)$-stability of backward difference formulae. BIT Numer. Math. 60, 93–99 (2020), https://doi.org/10.1007/s10543-019-00768-1
- Albrecht, P.: Explicit, optimal stability functionals and their application to cyclic discretization methods. Computing 19, 233–249 (1978), https://doi.org/10.1007/BF02252202
- Albrecht, P.: Numerical treatment of O.D.Es.: The theory of A-methods. Numer. Math. 47, 59–87 (1985), https://doi.org/10.1007/BF01389876
- Bickart, T.A., Picel, Z.: High order stiffly stable composite multistep methods for numerical integration of stiff differential equations. BIT Numer. Math. 13, 272–286 (1973), https://doi.org/10.1007/BF01951938
- Butcher, J.C.: Numerical Methods for Ordinary Differential Equations. John Wiley & Sons, Chichester (2016), https://doi.org/10.1002/9781119121534
- Gaffney, P.: A Performance Evaluation of Some FORTRAN Subroutines for the Solution of Stiff Oscillatory Ordinary Differential Equations. ACM Trans. Math. Softw. 10(1), 58–72 (1984), https://doi.org/10.1145/356068.356073
- Gohberg, I., Lancaster, P., Rodman, L.: Spectral Analysis of Matrix Polynomials — I. Canonical Forms and Divisors. Linear Algebra Its Appl. 20, 1–44 (1978), https://doi.org/10.1016/0024-3795%2878%2990026-5
- Gohberg, I., Lancaster, P., Rodman, L.: Matrix Polynomials. Society for Industrial and Applied Mathematics (2009), https://doi.org/10.1137/1.9780898719024
- Gupta, G.: Description and Evaluation of a Stiff ODE Code DSTIFF. SIAM J. Sci. Comput 6(4), 939–950 (1985), https://doi.org/10.1137/0906063
- Hairer, E., Wanner, G., Nørsett, S.: Solving Ordinary Differential Equations I – Nonstiff Problems. Springer Berlin, Heidelberg (2008), https://doi.org/10.1007/978-3-540-78862-1
- Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II – Stiff and Differential-Algebraic Problems. Springer Berlin, Heidelberg (2010), https://doi.org/10.1007/978-3-642-05221-7
- Mihelcic, M., Wingerath, K.: $A(\alpha)$-Stable Cyclic Composite Multistep Methods of Orders 6 and 7 for Numerical Integration of Stiff Ordinary Differential Equations. ZAMM 61, 261–264 (1981), https://doi.org/10.1002/zamm.19810610609
- Montenbruck, O., Gill, E.: Satellite Orbits. Springer Berlin, Heidelberg (2000), https://doi.org/10.1007/978-3-642-58351-3
- Nørsett, S., Thomsen, P.G.: Switching between modified Newton and fix-point iteration for implicit ode-solvers. BIT Numer. Math. 26, 339–348 (1986), https://doi.org/10.1007/BF01933714
- Petzold, L.: Automatic Selection of Methods for Solving Stiff and Nonstiff Systems of Ordinary Differential Equations. SIAM J. Sci. Comput. 4(1), 136–148 (1983), https://doi.org/10.1137/0904010
- Shampine, L.F.: Type-sensitive ODE codes based on implicit $A(\alpha)$-stable formulas. Math. Comput. 39(159), 109–123 (1982), https://doi.org/10.2307/2007622
- Skeel, R.: Analysis of Fixed-Stepsize Methods. SIAM J. Numer. Anal. 13(5), 664–685 (1976), https://doi.org/10.1137/0713055
- Städter, P., Schälte, Y., Schmiester, L., Hasenauer, J., Stapor, P.L.: Benchmarking of numerical integration methods for ODE models of biological systems. Scientific Reports 11, 2696 (2021), https://doi.org/10.1038/s41598-021-82196-2
- Tendler, J.M.: A Stiffly Stable Integration Process Using Cyclic Composite Methods. Ph.D. thesis, Syracuse University, Syracuse, New York (1973)
- Tendler, J.M., Bickart, T.A., Picel, Z.: STINT: STiff ordinary differential equations INTegrator. Program and User Manual. Electrical and Computer Engineering Department, Syracuse University, Syracuse, New York 13210, USA, and Department of Electrical Engineering, Delft University of Technology, Delft, The Netherlands, Technical Report TR-76-12 (1976)
- Tendler, J.M., Bickart, T.A., Picel, Z.: A Stiffly Stable Integration Process Using Cyclic Composite Methods. ACM Trans. Math. Softw. 4(4), 339–368 (1978), https://doi.org/10.1145/356502.356495
- Tischer, P.: The Cyclic Use of Linear Multistep Formulas for the Solution of Stiff Differential Equations. Ph.D. thesis, Department of Computer Science, Monash University, Clayton, Victoria, Australia (1983)
- Tischer, P., Sacks-Davis, R.: A New Class of Cyclic Multistep Formulae for Stiff Systems. SIAM J. Sci. Comput. 4(4), 733–747 (1983), https://doi.org/10.1137/0904051
- Tischer, P., Gupta, G.: An evaluation of some new cyclic linear multistep formulas for stiff ODEs. ACM Trans. Math. Softw. 11(3), 263–270 (1985), https://doi.org/10.1145/214408.214417
- Werner, H., Arndt, H.: Gewöhnliche Differentialgleichungen. Springer Berlin, Heidelberg (1986), https://doi.org/10.1007/978-3-642-70338-6